本内容按照吴恩达公开课《Machine Learning》的 Lecture Slides 进行分类，每一个H1标题对应一个Lecture Slide，每一个H2标题对应Lecture Slide中的一个小章节。

本内容是课程的简化总结，适合已经了解机器学习基本概念的人进行回顾以及查漏补缺。

7 正则化

7.1 过拟合问题

过拟合：如果特征过多，模型可能对训练集有很好的效果，但泛化能力很差

线性回归例子：

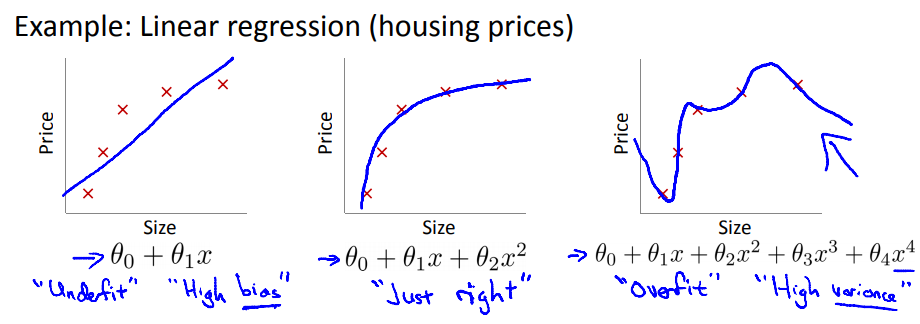
逻辑回归例子：

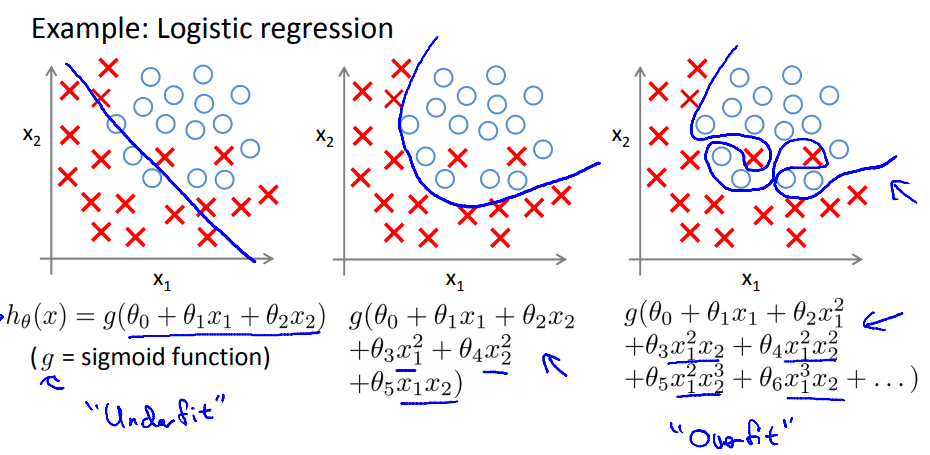
解决过拟合的方法：

1. 减少特征数量
   • 手工选取重要特征
   • 特征选择算法（后面会介绍）
2. 正则化
   • 保留所有特征，但是对参数 的量级加以限制
   • 当所有特征都对模型有一点点贡献的情况下，正则化很有效

7.2 带正则化项的损失函数

带L2正则化项的损失函数为：

其中的正则化项 限制了 的增长， 为正则化系数。

如果 选择过大，会导致模型欠拟合。

7.3 带正则化的线性回归

带正则化的梯度下降：

此时的梯度要同时考虑正则化项

梯度更新方程对于 是不变的，对于 就变成了：

可以看到L2正则化相当于给 的梯度更新方程增加了一个惩罚项，每次更新参数时都会对 进行一部分缩减，并且这个缩减量与三个系数相关。

带正则化的标准方程：

带正则化的标准方程为：

这个里面的矩阵是一个左上角元素为0的单位矩阵，维度为 (n+1)x(n+1)，n为特征个数

之前说过当 样本个数 m<n 时， 不可逆，但是这里当我们加入后面这项后，这个整个东西 就可逆了。

7.4 带正则化的逻辑回归

此时的Log损失函数变为：

梯度下降算法过程变为：