Simon’s Notebook

本内容按照吴恩达公开课《Machine Learning》的 Lecture Slides 进行分类，每一个H1标题对应一个Lecture Slide，每一个H2标题对应Lecture Slide中的一个小章节。

本内容是课程的简化总结，适合已经了解机器学习基本概念的人进行回顾以及查漏补缺。

# 6 逻辑回归

# 6.1 分类

逻辑回归用于分类问题的场景，例如：

  • 邮件是否是垃圾邮件？
  • 订单是否是欺诈订单？
  • 肿瘤是良性还是恶性？

此时 ，一般把0当作负例，1当作正例

阈值的选择：可以自定义，例如：

当 时，预测

当 时，预测

编者注1：后来我们知道阈值的选择会对应不同的模型表现，通过衡量模型在不同阈值下的总体表现，就产生了ROC曲线，通过计算ROC曲线下的面积，就产生了AUC评价指标。

编者注2：**为什么要使用逻辑回归呢？**通过线性函数拟合，然后选择恰当的阈值来得到结果不可以吗？可以，但是这样做有两个问题：一、阈值的选择会因此变得非常敏感；二、线性函数会因此无法很好地拟合数据。其实本质上来讲，使用sigmoid函数将连续空间转化到[0, 1]空间，就是为了更好地拟合数据分布的空间。

编者注3：进一步思考，如果采用线性模型，仅在损失的计算中应用sigmoid（例如logit loss），那么模型的拟合与逻辑回归其实是一样了，此时也可以通过选择一个恰当的y的阈值来定义模型。此时可以理解为把逻辑回归的sigmod层脱离了出来，这里的y就是逻辑回归中的隐藏层y（加sigmoid函数之前）

# 6.2 模型表示

在线性回归的基础上：增加一个函数 ，使得：

如果 使用Sigmoid函数(也叫Logistic函数)，则模型就叫逻辑回归(Logistic Regression)

于是，整个模型就是

由于逻辑回归的输出为(0, 1)空间，所以可以解释为概率值，例：如果 则一个病人的肿瘤为恶性的概率为70%。

# 6.3 决策边界的线性与非线性

当输入g(z)的模型函数为线性函数时，决策边界就是线性的。例如，输入线性函数情况下定义决策边界为0.5，则当 时， 就 ，此时 就是二维平面内划分正负样例的一条直线：

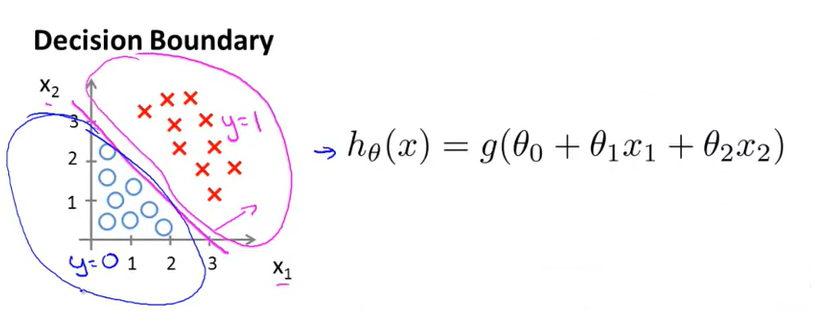
image-20200809201240355

当输入g(z)的函数为非线性函数时，决策边界就可以是非线性的。例如，当输入函数为 时，函数为抛物面，

img

此时的决策边界就可以是一个圆/椭圆：

image-20200809201847083

# 6.4 逻辑回归损失函数

逻辑回归的损失函数如下：

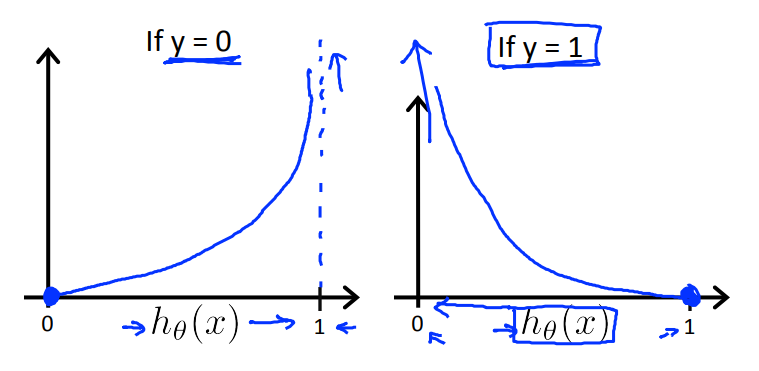
Cost(h_\theta{(x)},y)=\begin{cases}-log(h_\theta(x))&if\;y=1\\-log(1-h_\theta(x))&if\;y=0\end{cases}

其图像如下：

image-20200809204653140

# 6.5 简化损失函数与梯度下降

简化后的损失函数为：

同时考虑了y=1和y=0的情况，并且把负号提到了最前面。

编者注：这个损失函数就叫做Log损失或者Logistic损失或者Logit损失或者Logarithmic损失，都是同一个东西。参考: Reference (opens new window)

逻辑回归的梯度下降：

对求导，可得：

因此如果要最小化 ，算法为：

重复 直到函数收敛。

可以发现这个表达式和最小二乘法的线性回归几乎一样！

# 6.6 高级优化算法

除了梯度下降，还有一些更高级的优化算法，例如：

这些方法无需设定学习率，一般比梯度下降更快，但缺点是计算复杂度更高

在Octave中可以用fminunc函数来使用这些优化算法：

options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
   [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

# 6.7 多分类：一对多

对于多分类问题（大于等于3个类别），可以采用一对多方式，对每个类别都训练一个二分类模型（把当前类为1当作正类），然后在预测时把样本输入到每个模型中，最后选择的类别为最大的输出概率所对应的类别：

← 7.正则化 →